ImplicationalSystem (lattices 2.0.0-SNAPSHOT API)

java.lang.Object
- org.thegalactic.lattice.ClosureSystem
- - org.thegalactic.rule.ImplicationalSystem

```
public class ImplicationalSystem
extends ClosureSystem
```
This class gives a representation for an implicational system (ImplicationalSystem), a set of rules.

An ImplicationalSystem is composed of a TreeSet of comparable elements, and a TreeSet of rules defined by class Rule.

This class provides methods implementing classical transformation of an implicational system : make proper, make minimum, make right maximal, make left minimal, make unary, make canonical basis, make canonical direct basis and reduction.

An implicational system owns properties of a closure system, and thus extends the abstract class ClosureSystem and implements methods getSet() and closure(java.util.TreeSet<java.lang.Comparable>).

Therefore, the closed set lattice of an ImplicationalSystem can be generated by invoking method ClosureSystem.closedSetLattice(boolean) of a closure system.

An implicational system can be instancied from and save to a text file in the following format: - a list of elements separated by a space in the first line ; - then, each rule on a line, written like [premise] -> [conclusion] where elements are separated by a space.
```
a b c d e
a b -> c d
c d -> e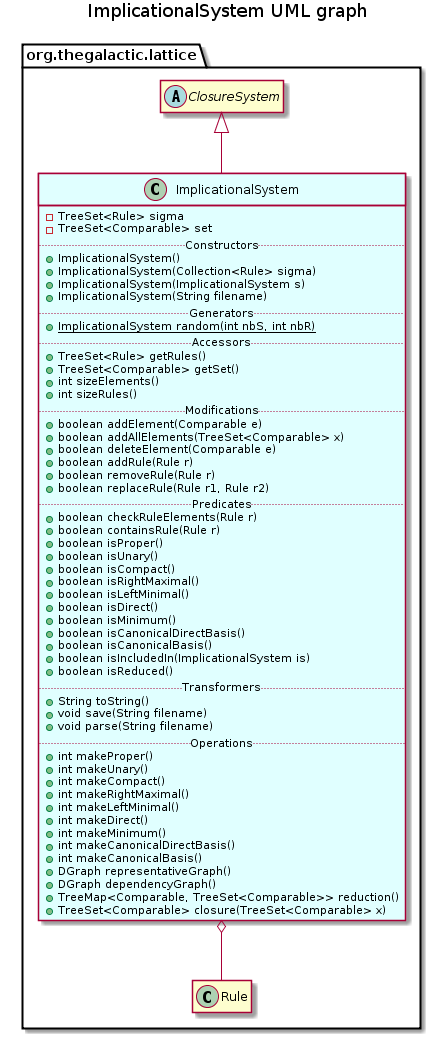
```

Constructor Summary

Constructors
Constructor and Description
`ImplicationalSystem()` Constructs a new empty component.
`ImplicationalSystem(Collection<Rule> sigma)` Constructs this component from the specified set of rules `sigma`.
`ImplicationalSystem(ImplicationalSystem is)` Constructs this component as a copy of the specified ImplicationalSystem `is`.
`ImplicationalSystem(String filename)` Constructs this component from the specified file.

Method Summary

All Methods Static Methods Instance Methods Concrete Methods
Modifier and Type	Method and Description
`boolean`	`addAllElements(TreeSet<Comparable> x)` Adds the specified element to the set `S` of this component.
`boolean`	`addElement(Comparable e)` Adds the specified element to the set `S` of this component.
`boolean`	`addRule(Rule rule)` Adds the specified rule to this component.
`boolean`	`checkRuleElements(Rule rule)` Checks if the set S of this component contains the elements of the specified rule.
`TreeSet<Comparable>`	`closure(TreeSet<Comparable> x)` Builds the closure of a set X of indexed elements.
`boolean`	`containsRule(Rule rule)` Checks if this component already contains the specified rule.
`boolean`	`deleteElement(Comparable e)` Delete the specified element from the set `S` of this component and from all the rule containing it.
`ConcreteDGraph`	`dependencyGraph()` Returns the dependency graph of this component.
`SortedSet<Rule>`	`getRules()` Returns the set of rules.
`SortedSet<Comparable>`	`getSet()` Returns the set of indexed elements.
`ImplicationalSystem`	`init()` Initialise the implicational system.
`boolean`	`isCanonicalBasis()` Returns true if this component is equal to its canonical basis.
`boolean`	`isCanonicalDirectBasis()` Returns true if this component is equal to its canonical direct basis.
`boolean`	`isCompact()` Returns true if this component is a compact ImplicationalSystem.
`boolean`	`isDirect()` Returns true if this component is direct.
`boolean`	`isIncludedIn(ImplicationalSystem is)` Compares by inclusion of the proper and unary form of this component with the specified one.
`boolean`	`isLeftMinimal()` Returns true if this component is left minimal.
`boolean`	`isMinimum()` Returns true if this component is minimum.
`boolean`	`isProper()` Returns true if this component is a proper ImplicationalSystem.
`boolean`	`isReduced()` Return true if this component is reduced.
`boolean`	`isRightMaximal()` Returns true if conclusion of rules of this component are closed.
`boolean`	`isUnary()` Returns true if this component is an unary ImplicationalSystem.
`int`	`makeCanonicalBasis()` Replace this component by the canonical basis.
`int`	`makeCanonicalDirectBasis()` Replace this component by its canonical direct basis.
`int`	`makeCompact()` Replaces rules of same premise by only one rule.
`int`	`makeCompactAssociation()` Replaces association rules of same premise, same support and same confidence by only one rule.
`int`	`makeDirect()` Makes this component a compact and direct ImplicationalSystem.
`int`	`makeLeftMinimal()` Makes this component a left minimal and compact ImplicationalSystem.
`int`	`makeMinimum()` Makes this component a minimum and proper ImplicationalSystem.
`int`	`makeProper()` Makes this component a proper ImplicationalSystem.
`int`	`makeRightMaximal()` Replaces conclusion of each rule with their closure without the premise.
`int`	`makeUnary()` Makes this component an unary ImplicationalSystem.
`ImplicationalSystem`	`parse(String filename)` Parse the description of this component from a file whose name is specified.
`static ImplicationalSystem`	`random(int nbS, int nbR)` Generates a random ImplicationalSystem with a specified number of nodes and rules.
`TreeMap<Comparable,TreeSet<Comparable>>`	`reduction()` Removes from this component reducible elements.
`boolean`	`removeRule(Rule rule)` Removes the specified rule from the set of rules of this component.
`boolean`	`replaceRule(Rule rule1, Rule rule2)` Replaces the first specified rule by the second one.
`ConcreteDGraph`	`representativeGraph()` Returns the representative graph of this component.
`void`	`save(String filename)` Save the description of this component in a file whose name is specified.
`int`	`sizeElements()` Returns the number of elements in the set S of this component.
`int`	`sizeRules()` Returns the number of rules of this component.
`String`	`toString()` Returns a string representation of this component.

Methods inherited from class org.thegalactic.lattice.ClosureSystem
allClosures, closedSetLattice, getReducibleElements, lattice, nextClosure, precedenceGraph

Methods inherited from class java.lang.Object
clone, equals, finalize, getClass, hashCode, notify, notifyAll, wait, wait, wait

- Constructor Detail
  - ImplicationalSystem
```
public ImplicationalSystem()
```
    Constructs a new empty component.
  - ImplicationalSystem
```
public ImplicationalSystem(Collection<Rule> sigma)
```
    Constructs this component from the specified set of rules sigma.
    
    Parameters:
    
    sigma - the set of rules.
  - ImplicationalSystem
```
public ImplicationalSystem(ImplicationalSystem is)
```
    Constructs this component as a copy of the specified ImplicationalSystem is.
    
    Only structures (conataining reference of indexed elements) are copied.
    
    Parameters:
    
    is - the implicational system to be copied
  - ImplicationalSystem
```
public ImplicationalSystem(String filename)
                    throws IOException
```
    Constructs this component from the specified file.
    
    The file have to respect a certain format:
    
    An implicational system can be instancied from and save to a text file in the following format: - A list of elements separated by a space in the first line ; - then, each rule on a line, written like [premise] -> [conclusion] where elements are separated by a space.
```
a b c d e a b -> c d c d -> e
```
    Each element must be declared on the first line, otherwise, it is not added in the rule Each rule must have a non empty concusion, otherwise, it is not added in the component
    Parameters:
    
    filename - the name of the file
    
    Throws:
    
    IOException - When an IOException occurs
- Method Detail
  - random
```
public static ImplicationalSystem random(int nbS,
                                         int nbR)
```
    Generates a random ImplicationalSystem with a specified number of nodes and rules.
    
    Parameters:
    
    nbS - the number of nodes of the generated ImplicationalSystem
    
    nbR - the number of rules of the generated ImplicationalSystem
    
    Returns:
    
    a random implicational system with a specified number of nodes and rules.
  - init
```
public ImplicationalSystem init()
```
    Initialise the implicational system.
    
    Returns:
    
    this for chaining
  - getRules
```
public SortedSet<Rule> getRules()
```
    Returns the set of rules.
    
    Returns:
    
    the set of rules of this component.
  - getSet
```
public SortedSet<Comparable> getSet()
```
    Returns the set of indexed elements.
    
    Specified by:
    
    getSet in class ClosureSystem
    
    Returns:
    
    the elements space of this component.
  - sizeElements
```
public int sizeElements()
```
    Returns the number of elements in the set S of this component.
    
    Returns:
    
    the number of elements in the elements space of this component.
  - sizeRules
```
public int sizeRules()
```
    Returns the number of rules of this component.
    
    Returns:
    
    the number of rules of this component.
  - addElement
```
public boolean addElement(Comparable e)
```
    Adds the specified element to the set S of this component.
    
    Parameters:
    
    e - the comparable to be added
    
    Returns:
    
    true if the element has been added to S
  - addAllElements
```
public boolean addAllElements(TreeSet<Comparable> x)
```
    Adds the specified element to the set S of this component.
    
    Parameters:
    
    x - the treeset of comparable to be added
    
    Returns:
    
    true if the element has been added to S
  - deleteElement
```
public boolean deleteElement(Comparable e)
```
    Delete the specified element from the set S of this component and from all the rule containing it.
    
    Parameters:
    
    e - the comparable to be added
    
    Returns:
    
    true if the element has been added to S
  - checkRuleElements
```
public boolean checkRuleElements(Rule rule)
```
    Checks if the set S of this component contains the elements of the specified rule.
    
    Parameters:
    
    rule - the rule to be checked
    
    Returns:
    
    true if S contains all the elements of the rule
  - containsRule
```
public boolean containsRule(Rule rule)
```
    Checks if this component already contains the specified rule.
    
    Rules are compared according to their premise and conclusion
    
    Parameters:
    
    rule - the rule to be tested
    
    Returns:
    
    true if sigma contains the rule
  - addRule
```
public boolean addRule(Rule rule)
```
    Adds the specified rule to this component.
    
    Parameters:
    
    rule - the rule to be added
    
    Returns:
    
    true the rule has been added to if sigma
  - removeRule
```
public boolean removeRule(Rule rule)
```
    Removes the specified rule from the set of rules of this component.
    
    Parameters:
    
    rule - the rule to be removed
    
    Returns:
    
    true if the rule has been removed
  - replaceRule
```
public boolean replaceRule(Rule rule1,
                           Rule rule2)
```
    Replaces the first specified rule by the second one.
    
    Parameters:
    
    rule1 - the rule to be replaced by rule2
    
    rule2 - the replacing rule
    
    Returns:
    
    true the rule has been replaced
  - toString
```
public String toString()
```
    Returns a string representation of this component.
    
    The following format is used:
    
    An implicational system can be instancied from and save to a text file in the following format: - A list of elements separated by a space in the first line ; - then, each rule on a line, written like [premise] -> [conclusion] where elements are separated by a space.
```
a b c d e
a b -> c
d c d -> e
```
    Overrides:
    
    toString in class Object
    
    Returns:
    
    a string representation of this component.
  - save
```
public void save(String filename)
          throws IOException
```
    Save the description of this component in a file whose name is specified.
    
    Specified by:
    
    save in class ClosureSystem
    
    Parameters:
    
    filename - the name of the file
    
    Throws:
    
    IOException - When an IOException occurs
  - parse
```
public ImplicationalSystem parse(String filename)
                          throws IOException
```
    Parse the description of this component from a file whose name is specified.
    
    Parameters:
    
    filename - the name of the file
    
    Returns:
    
    this for chaining
    
    Throws:
    
    IOException - When an IOException occurs
  - isProper
```
public boolean isProper()
```
    Returns true if this component is a proper ImplicationalSystem.
    
    This test is perfomed in O(|Sigma||S|) by testing conclusion of each rule
    
    Returns:
    
    true if and only if this component is a proper implicational system.
  - isUnary
```
public boolean isUnary()
```
    Returns true if this component is an unary ImplicationalSystem.
    
    This test is perfomed in O(|Sigma||S|) by testing conclusion of each rule
    
    Returns:
    
    true if this component is an unary ImplicationalSystem.
  - isCompact
```
public boolean isCompact()
```
    Returns true if this component is a compact ImplicationalSystem.
    
    This test is perfomed in O(|Sigma|^2|S|) by testing premises of each pair of rules
    
    Returns:
    
    true if this component is a compact ImplicationalSystem.
  - isRightMaximal
```
public boolean isRightMaximal()
```
    Returns true if conclusion of rules of this component are closed.
    
    This test is perfomed in O(|Sigma||S|) by testing conclusion of each rule
    
    Returns:
    
    true if conclusion of rules of this component are closed.
  - isLeftMinimal
```
public boolean isLeftMinimal()
```
    Returns true if this component is left minimal.
    
    This test is perfomed in O(|Sigma|^2|S|) by testing conclusions of each pair of rules
    
    Returns:
    
    true if this component is left minimal.
  - isDirect
```
public boolean isDirect()
```
    Returns true if this component is direct.
    
    This test is perfomed in O(|Sigma|^2|S|) by testing if closure of the premisse of each conclusion can be obtained by only one iteration on the set of rules.
    
    Returns:
    
    true if this component is direct.
  - isMinimum
```
public boolean isMinimum()
```
    Returns true if this component is minimum.
    
    This test is perfomed in O(|Sigma|^2|S|) by testing if closure of the premisse of each conclusion can be obtained by only one iteration on the set of rules.
    
    Returns:
    
    true if this component is minimum.
  - isCanonicalDirectBasis
```
public boolean isCanonicalDirectBasis()
```
    Returns true if this component is equal to its canonical direct basis.
    
    The canonical direct basis is computed before to be compare with this component.
    
    This test is performed in O(d|S|), where d corresponds to the number of rules that have to be added by the direct treatment. This number is exponential in the worst case.
    
    Returns:
    
    true if this component is equal to its canonical direct basis.
  - isCanonicalBasis
```
public boolean isCanonicalBasis()
```
    Returns true if this component is equal to its canonical basis.
    
    The canonical basis is computed before to be compare with this component.
    
    This treatment is performed in (|Sigma||S|cl) where O(cl) is the computation of a closure.
    
    Returns:
    
    true if this component is equal to its canonical basis.
  - isIncludedIn
```
public boolean isIncludedIn(ImplicationalSystem is)
```
    Compares by inclusion of the proper and unary form of this component with the specified one.
    
    Parameters:
    
    is - another ImplicationalSystem
    
    Returns:
    
    true if really include in this componenet.
  - makeProper
```
public int makeProper()
```
    Makes this component a proper ImplicationalSystem.
    
    Elements that are at once in the conclusion and in the premise are deleted from the conclusion. When the obtained conclusion is an empty set, the rule is deleted from this component
    
    This treatment is performed in O(|Sigma||S|).
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeUnary
```
public int makeUnary()
```
    Makes this component an unary ImplicationalSystem.
    
    This treatment is performed in O(|Sigma||S|)
    
    A rule with a non singleton as conclusion is replaced with a sets of rule, one rule for each element of the conclusion.
    
    This treatment is performed in O(|Sigma||S|).
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeCompact
```
public int makeCompact()
```
    Replaces rules of same premise by only one rule.
    
    This treatment is performed in O(|sigma|^2|S|)
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeCompactAssociation
```
public int makeCompactAssociation()
```
    Replaces association rules of same premise, same support and same confidence by only one rule.
    
    This treatment is performed in O(|sigma|^2|S|)
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeRightMaximal
```
public int makeRightMaximal()
```
    Replaces conclusion of each rule with their closure without the premise.
    
    This treatment is performed in O(|sigma||S|cl), where O(cl) is the computation of a closure.
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeLeftMinimal
```
public int makeLeftMinimal()
```
    Makes this component a left minimal and compact ImplicationalSystem.
    
    The unary form of this componant is first computed: if two rules have the same unary conclusion, the rule with the inclusion-maximal premise is deleted.
    
    Then, the left-minimal treatment is performed in O(|sigma|^2|S|))
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeDirect
```
public int makeDirect()
```
    Makes this component a compact and direct ImplicationalSystem.
    
    The unary and proper form of this componant is first computed. For two given rules rule1 and rule2, if the conclusion of rule1 contains the premise of rule1, then a new rule is addes, with rule1.premisse + rule2.premisse - rule1.conclusion as premise, and rule2.conclusion as conlusion. This treatment is performed in a recursive way until no new rule is added.
    
    This treatment is performed in O(d|S|), where d corresponds to the number of rules that have to be added by the direct treatment, that can be exponential in the worst case.
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeMinimum
```
public int makeMinimum()
```
    Makes this component a minimum and proper ImplicationalSystem.
    
    A rule is deleted when the closure of its premisse remains the same even if this rule is suppressed.
    
    This treatment is performed in O(|sigma||S|cl) where O(cl) is the computation of a closure.
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeCanonicalDirectBasis
```
public int makeCanonicalDirectBasis()
```
    Replace this component by its canonical direct basis.
    
    The proper, unary and left minimal form of this component is first computed, before to apply the recursive directe treatment, then the left minimal treatment.
    
    This treatment is performed in O(d), where d corresponds to the number of rules that have to be added by the direct treatment. This number is exponential in the worst case.
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - makeCanonicalBasis
```
public int makeCanonicalBasis()
```
    Replace this component by the canonical basis.
    
    Conclusion of each rule is first replaced by its closure. Then, premise of each rule r is replaced by its closure in ImplicationalSystem \ rule. This treatment is performed in (|Sigma||S|cl) where O(cl) is the computation of a closure.
    
    Returns:
    
    the difference between the number of rules of this component before and after this treatment
  - representativeGraph
```
public ConcreteDGraph representativeGraph()
```
    Returns the representative graph of this component.
    
    Nodes of the graph are attributes of this components. For each proper rule X+b->a, there is an {X}-valuated edge from a to b. Notice that, for a rule b->a, the edge from a to b is valuated by emptyset. and for the two rules X+b->a and Y+b->a, the edge from a to b is valuated by {X,Y}.
    
    Returns:
    
    the representative graph of this component.
  - dependencyGraph
```
public ConcreteDGraph dependencyGraph()
```
    Returns the dependency graph of this component.
    
    Dependency graph of this component is the representative graph of the canonical direct basis. Therefore, the canonical direct basis has to be generated before to compute its representativ graph, and this treatment is performed in O(d), as for the canonical direct basis generation, where d corresponds to the number of rules that have to be added by the direct treatment. This number is exponential in the worst case.
    
    Returns:
    
    the dependency graph of this component.
  - reduction
```
public TreeMap<Comparable,TreeSet<Comparable>> reduction()
```
    Removes from this component reducible elements.
    
    Reducible elements are elements equivalent by closure to others elements. They are computed by getReducibleElements of ClosureSystem in O(O(|Sigma||S|^2)
    
    Returns:
    
    the set of reducibles removed elements, with their equivalent elements
  - isReduced
```
public boolean isReduced()
```
    Return true if this component is reduced.
    
    Returns:
    
    true if this component is reduced.
  - closure
```
public TreeSet<Comparable> closure(TreeSet<Comparable> x)
```
    Builds the closure of a set X of indexed elements.
    
    The closure is initialised with X. The closure is incremented with the conclusion of each rule whose premise is included in it. Iterations over the rules are performed until no new element has to be added in the closure.
    
    For direct ImplicationalSystem, only one iteration is needed, and the treatment is performed in O(|Sigma||S|).
    
    For non direct ImplicationalSystem, at most |S| iterations are needed, and this tratment is performed in O(|Sigma||S|^2).
    
    Specified by:
    
    closure in class ClosureSystem
    
    Parameters:
    
    x - a TreeSet of indexed elements
    
    Returns:
    
    the closure of X for this component

Class ImplicationalSystem

Constructor Summary

Method Summary

Methods inherited from class org.thegalactic.lattice.ClosureSystem

Methods inherited from class java.lang.Object

Constructor Detail

ImplicationalSystem

ImplicationalSystem

ImplicationalSystem

ImplicationalSystem

Method Detail

random

init

getRules

getSet

sizeElements

sizeRules

addElement

addAllElements

deleteElement

checkRuleElements

containsRule

addRule

removeRule

replaceRule

toString

save

parse

isProper

isUnary

isCompact

isRightMaximal

isLeftMinimal

isDirect

isMinimum

isCanonicalDirectBasis

isCanonicalBasis

isIncludedIn

makeProper

makeUnary

makeCompact

makeCompactAssociation

makeRightMaximal

makeLeftMinimal

makeDirect

makeMinimum

makeCanonicalDirectBasis

makeCanonicalBasis

representativeGraph

dependencyGraph

reduction

isReduced

closure